井字棋与最大最小值算法
经过昨晚,和今天早上 8 点醒来趴在床上努力的思考。我终于想起了如何使用数学归纳法证明策梅洛定理。然后经过一上午的努力,我成功使用最大最小值算法实现了井字棋 (Tic-Tak-Toe) 的 AI,然后添加到 wwh 的井字棋代码中。
数学归纳法证明策梅洛定理¶
策梅洛定理:
条件:
- 游戏双方拥有完全信息(即一方明确另一方的每一个行动所产生的所有后果)
- 游戏的规则不包含随机性
- 游戏必定在有限步内结束
结论:
- 先手或后手存在必不败策略(如果游戏只包含胜,负两种情况,则结论为:先手或后手存在必胜策略)
proof:
对满足上述要求的一个游戏,假设游戏的有限步数最大为 N,以下用数学归纳法证明对任意非零自然数 N,结论成立。
-
当 N=1 时,由于先手行动一步游戏便结束,因此存在几种可能:
- 存在先手赢或平的结局,因此无论是否存在后手赢的结局,先手必然选择不败的结局。即先手存在必不败策略。 - 不存在先手赢或平的结局,即所有结局均为后手赢。后手存在必胜策略。
均符合假设。
-
假设当 N=k 时也成立,则当 N=k+1 时。对于先手的每一种行动,在该条件下可形成一个“子游戏”,且该游戏行动步数上限为 k。因此按照结论,可能的情况为:
- 所有“子游戏”中存在一个使得先手存在必不败策略。则先手必然会选择对应行动产生该子游戏。即先手存在必不败策略。 - 所有“子游戏”均不存在先手必不败策略,按照结论,则必然均存在后手必不败策略。则原游戏后手存在必不败策略。
因此 N=k+1 时结论也成立(这里说明的后手存在必胜策略,则必然存在必不败策略)
Q.E.D
此定理的结论十分有力,它表明一个游戏从规则制定完成后,结局就已经确定了。因为如果游戏是一方必赢的,那么理论上无论另一方怎么努力都永远都只能败北。而如果游戏是一方至少能保证平局的,那么同样无论另一方怎么努力也只能和对方打成平手。
然而该定理虽然说明了存在这种策略,但并没有给出策略是什么?是怎么一种“形式”?究竟怎么才能按照策略来走呢?
HOWERVER,这样的策略事实上一点也不抽象,而且按照策略走的方法也非常简单!!!答案就是最大最小值算法!!!
最大最小值算法¶
步骤¶
-
首先,游戏双方的所有可能行动可以抽象成一个一颗决策树。双方的不同行动产生不同的分支。直至某一方的行动导致游戏结束,并形成一个叶节点。
-
我们以先手为视角,把决策树的每个叶子节点标上一个值,胜记为 1,负为 -1,平为 0。
-
我们知道第 0 层(根节点)为先手的决策层。由于双方轮流决策,易知,偶数层为先手决策层,我们把它称为 MAX 层。同理,奇数层称为 MIN 层。
-
接着我们开始自底向上遍历决策树。对于每个 MIN 层的结点,我们将其子节点中的最小值赋值给该节点。对于每个 MAX 层的结点,我们将其子节点中的最大值赋值给该节点。最终,我们能得根节点的值。
根节点值的含义¶
- 为 1,这表明先手存在必胜策略。
- 为 0,这表明先手存在必平策略,后手怎么也不可能赢先手。
- 为 -1,这表明只要后手足够“聪明”,每次都能下最“正确“的棋(MIN 层使节点值最小),那么先手必败。
原理¶
非严格地分析,我们考虑下图的情形,方形代表 MAX 层,圆形代表 MIN 层。
最后能够证明对任意层,该层节点的值表示,先手存在策略使得在该“形势”下,先手最终“收益”(把 +1、-1、0 看做对先手“形势”的评分)不低于该值。严格证明可以对层数使用数学归纳法。
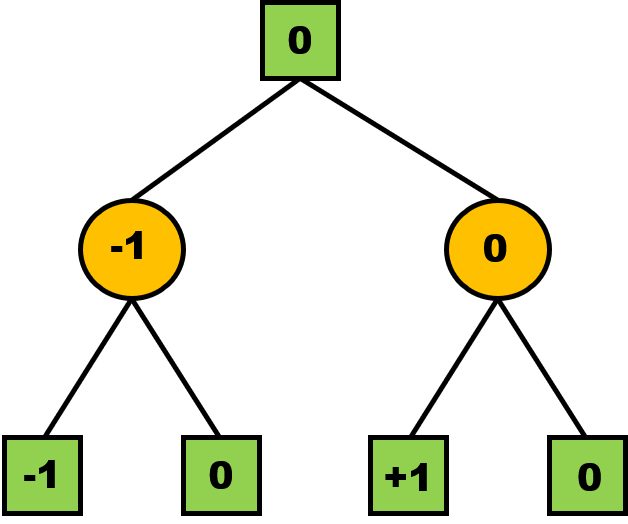
意义¶
可以看出,只要我们构造出了这颗完整的树,把它保存成一个文件。那么进行游戏时,我们便只是从上往下选择一条边这么简单。(在自底向上遍历树的同时,除了把值赋给每层节点,还可以把选择的下一个节点也存储下来,那么此时选择的时间复杂度就是 O(1))
因此,我们从理论上是证明了策梅洛定理匪夷所思的结论,并且还给出了可以说是一种“可执行”的方法。然而,数学上的可行在实际上却未必可行。以五子棋为例,棋盘为\(15 \times 15 =225\)格,如果采用上述算法,这个树最多会有:
这个数量级的边或者节点。
作为对比,宇宙原子总数不超过\(10^{100}\),而目前超级计算机的计算能力还未达到 EFLOPS 数量级,即每秒进行\(10^{18}\)次浮点运算。可以想象,上面的数量级是多么遥不可及的存在。
不过幸好,井字棋的可能性只有\(9! = 362880\),采用上面的算法是完全可行的。文末附代码。
alpha-beta 剪枝算法¶
上面的算法直接生成完整的树,然后再完整遍历仅用于说明原理。事实上我们可以引进一个 Level 变量,用于控制计算机的“聪明”程度。以下是不同的地方:
- 树不必提前生成,而在在进行决策的时候才往下生长 Level 层。(减少内存开销)
- 需要引入评分函数,合理地对各个“形势”进行评分。之前只对胜负平三种情况进行了评分。
- alpha-beta 剪枝算法进行搜索。不必自底向上完整遍历生成的树。
参考资料:alpha-beta 剪枝算法 - 加利福尼亚大学洛杉矶分校
井字棋 python 代码¶
完整代码下载:TicTacToe.py
关键代码:
def gen_game_tree(board, choices, player):
'''
generate the all possibility game tree when the specific player play the first within the given board and choices
the leaf node value is the result related to the specific player: player-> win, -player-> lose, 0 tie
board: list, numerical board
choices: list, the possible move index
player: int, -1 or 1(not the char 'X' or 'O')
return: dict, the game tree, like {1:{...}, 2:-1, ...}
'''
if len(choices)==0:
return 0 # no winner
#DSF
tree = {}
for i in range(len(choices)):
#make copy
choices_next = choices[:]
board_next = board[:]
del choices_next[i]
makeMove(board_next, player, choices[i])
if isWinner(board_next, player):
tree[choices[i]]= player
else:
tree[choices[i]]=gen_game_tree(board_next, choices_next, -player)
return tree
def maxminmize(tree, isMAX):
'''
Search the tree and generate the internal-node value. since there is no Level restriction, the
computer will search the whole tree. So you will never win the computer in this game!!!
isMAX: bool, whether is the MAX layer. MAX mean the first player, need to maximize his value.
MIN mean the latter player, need to minimize the first player value.
'''
if type(tree)==int:
return tree
if isMAX:
the_max = -2 # negative infinite (compare to -1, 0, 1)
for move, subtree in tree.items():
value = maxminmize(subtree, not isMAX)
if value > the_max:
the_max = value
the_move = move
tree[0]=[the_move, the_max] #since 0 is not in 1~9, use it to record the max or min value.
else:
the_min = 2 # infinite (compare to -1, 0, 1)
for move, subtree in tree.items():
value = maxminmize(subtree, not isMAX)
if value < the_min:
the_min = value
the_move = move
tree[0]=[the_move, the_min] #since 0 is not in 1~9, use it to record the max or min value.
return tree[0][1]