使用整数位运算计算 div10

使用整数位运算计算 div10，得到舍入到整数的精确值。得到了一个 magic number

unsigned int div10(unsigned short x){
 //return x/10
 unsigned int t = x<<16;
 t = (t>>4) + (t>>5);
 t = t + (t>>4) + (t>>8) + (t>>12) + (t>>16);

 t += 6554;  //should in [409.6, 6553.6]
 unsigned int r;
 r = t>>16;
 return r;
}

1

1/10 二进制序列为 0.0001100110011...

因此主要思路是通过计算以下级数的前若干项来获得\(x \over 10\)的近似值：

\[ {x \over 10} = {x \over 2^4} + {x \over 2^5} + {x \over 2^8} + {x \over 2^9} + {x \over 2^{12}} + {x \over 2^{13}} + {x \over 2^{16}} + {x \over 2^{17}} + {x \over 2^{20}} + {x \over 2^{21}} +... \]

然而计算上述式子时，因为每一项采用的是整数右移的方式，因此每一项保留成整数时都会产生舍入误差，累加起来后会产生很大的误差。解决这个问题的一个好方法是先将整数左移若干位得到\(x^{\prime}\)：

\[ x^{\prime} = x << k \]

这样将\(x^{\prime}\)右移 k 位以内时，结果仍是整数。将每项累加后，再右移 k 位即可还原为原本结果。

此时我们计算的过程如下：

\[ x^{\prime} = x << k\\ t = \sum_{i=1}^{n}{({x^{\prime} \over 2^{4i}}+{x^{\prime} \over 2^{4i+1}})}\\ r = t >> k \\ k \ge 4n+1 \]

2

接下来要考虑精度的问题，当我们计算 t 时，由于截断会产生误差，可以算得：

\[ \Delta = \sum_{i=n+1}^{\infin}{({x^{\prime} \over 2^{4i}}+{x^{\prime} \over 2^{4i+1}})}\\ \Rightarrow \Delta = {x^{\prime} \over 2^{4n+1}}\cdot{1 \over 5} \]

即：

\[ t = {x^{\prime} \over 10} - \Delta \]

进一步可得：

\[ r = {x \over 10} - {x \over 2^{4n+1}}\cdot{1 \over 5} \]

3

由于 x 是 16 位 unsigend short 类型，因此

\[ 0 \le x \le 2^{16}-1 \]

当 n 取 4 时，可得 r 与 x/10 的偏差最大时 (x 取最大) 为\(0.1 - \sigma\)，小于 0.1（\(\sigma 是由于 x 取不到 2^{16}导致的\)）

由于 r 和 x/10 的误差已经小于 0.1 了，易知当 x/10 非整除时，x/10 和 r 向下取整到同一个整数。

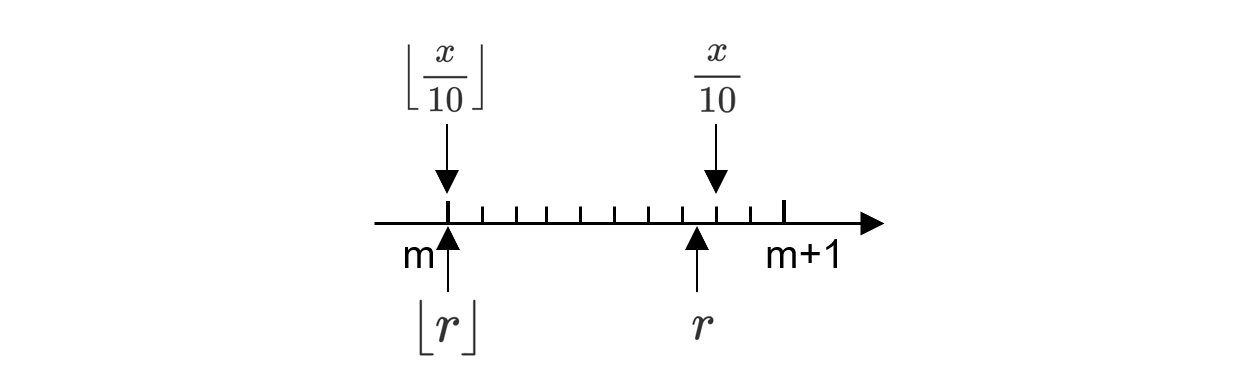
4

上面的方法在 x 不是 10 的倍数时，已经可以得到正确的值了。不过为了得到完全正确的结果，还需要进一步修正。

一个思路是在 x 整除 10 时进行 +1 修正，这里也有很多骚操作。

不过还有一个更好的方式，是对计算出的 r 增加一个偏移：

\[ r^{\prime} = r + \delta \]

使之满足：

\[ {x \over 10} \le r^{\prime}< {x \over 10}+0.1 \]

这样便可以保证\(r^{\prime}\)向下取整后取得正确的值。

代入 r 的式子计算后得：

\[ {x \over 2^{4n+1}}\cdot{1 \over 5} \le \delta \lt {1 \over 10} + {x \over 2^{4n+1}}\cdot{1 \over 5} \]

需要注意的是，上式要对任意的 x 都成立的。

当 x=0 时，可以得到\(\delta\)的上界，而\(\delta\)的下界由 x 的最大值确定，可得：

\[ {2^{16} - 1 \over 2^{4n+1}}\cdot{1 \over 5} \le \delta \lt {1 \over 10} \]

事实上对\(r\)添加偏移是为了易于说明，实际上我们是在计算得到的整数\(t\)​​​上增加一个整数偏移：

\[ t^{\prime} = t + \delta \]

由上面的分析，可得下式，其中\(\delta\)取整数：

\[ {2^{16} - 1 \over 2^{4n+1}}\cdot{1 \over 5}*2^{16} \le \delta \lt {1 \over 10}*2^{16} \]

可以发现，当 n=4 时，\(\delta\)无整数解

所以 n 需要取 5 以上，当 n=5 时，得：

\[ 409.59375 \le \delta \lt 6553.6 \]

最后的计算过程为：

\[ x^{\prime} = x <<16\\ t = \sum_{i=1}^{5}{({x^{\prime} \over 2^{4i}}+{x^{\prime} \over 2^{4i+1}})} + 410\\ r = t >> 16 \\ \]

虽然 n=5 时，左移 16 位，并不能保证计算 t 的过程中，没有舍入误差，好在该误差比较小，对最后结果没有造成太大影响。经实验后，实际最后的\(\delta\)取值可为\([410, 6554]\)，和理论分析仅差 1。