CUDA 优化

SC07¶

Microsoft PowerPoint - SC07_Optimization_Harris.ppt [Read-Only] (polytechnique.fr)

常见优化方法¶

优化目标

对于计算密集应用：峰值性能 GFLOP/s
对于访存密集应用：峰值带宽 bandwidth

二叉规约¶

是 memory bound 应用：

计算强度很低（1 flop/operator）

1: interleaved_addressing v1: 每个线程读取一个元素到 SMEM，然后二叉规约（stride）

__global__ void reduce0(int *g_idata, int *g_odata){
  extern __shared__ int sdata[];

  int tid = threadIdx.x;
  int i = blockIdx.x*blockDim.x + threadIdx.x;
  // each thread loads one element from global to shared mem
  sdata[tid] = g_idata[i];
  __syncthreads();

  //do reduction in SMEM
  for(int s=1; s<blockDim.x; s*=2){
    if(tid %(2*s)==0){
      sdata[tid] += sdata[tid + s];
    }
    __syncthreads();
  }

  //write result for this block to GMEM
  if(tid==0) g_odata[blockIdx.x] = sdata[0];
}

线程分支 diverge 太多如图，假设一个 warp 包含两个线程。则图中 8 个线程需要 4 个 warp。而即使一个 warp 里只有一个线程，仍然需要占用一个 warp。因此上面的算法会导致 4+4+2+1=11 次 warp 调用。 v2 版本的代码则一个 warp 里的两个线程都是工作的，需要 4+2+1+1=8 次（盗图自：http://home.ustc.edu.cn/~shaojiemike/posts/nvidiaoptimize/）

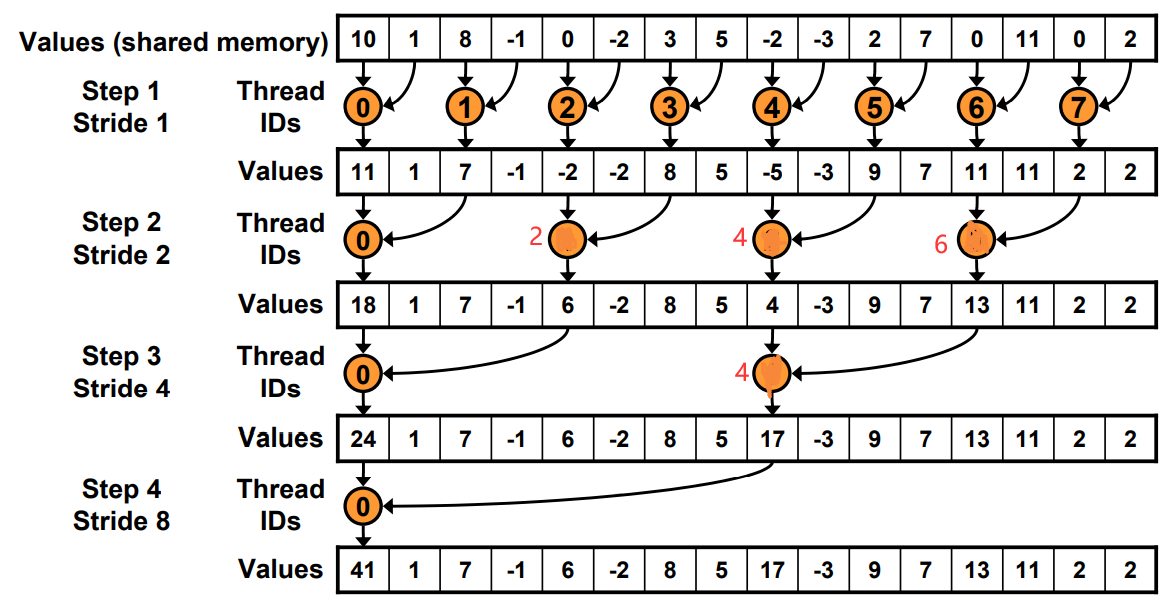
2: interleaved_addressing v2:

for(int s=1; s<blockDim.x; s*=2){
  int index = 2*s*tid;
  if(index < blockDim.x){
    sdata[index] += sdata[index+s];
  }
  __syncthreads();
}

SMEM bank conflict
3: sequential addressing

for(int s=blockDim.x/2; s>0; s>>=1){
  if(tid < s){
    sdata[tid] += sdata[tid+s];
  }
  __syncthreads();
}

第一次迭代就已经一半的线程是空闲的
4: first add during load：
- 仍然达不到带宽上限，因此可能是指令开销
  - 辅助类指令 (ancillary)：不是 load, store 和核心计算的算数指令
  - 即地址计算和循环开销

<<<n/64/2, 64>>>kernel();

int i = blockIdx.x * (blockDim.x*2) + threadIdx.x;
sdata[tid] = g_idata[i] + g_idata[i + blockDim.x];

5：Unroll the last warp
- 活动线程数随着规约迭代次数增加而减少
- 当 s<=32 时，只有一个 warp。warp 内的指令时 SIMD 同步的。
  - 因此不需要__syncthread()，不需要 if(tid < s)

for(int s=blockDim.x/2; s>32; s>>=1){
  if(tid < s){
    sdata[tid] += sdata[tid+s];
  }
  __syncthreads();
}
if(tid<32){
  sdata[tid] = sdata[tid+32];
  sdata[tid] = sdata[tid+16];
  sdata[tid] = sdata[tid+8];
  sdata[tid] = sdata[tid+4];
  sdata[tid] = sdata[tid+2];
  sdata[tid] = sdata[tid+1];
}

6: completely Unrolled
- 对于固定大小的线程块，可以完全展开。而 GPU 线程块的大小是 2 的幂，并且<1024。
- 可以使用模板，针对不同的线程块完全展开

template<int blockSize>
__global__ void reduce5(int *g_idata, int *g_odata)

if(blockSize>=512){
  if(tid<256){sdata[tid]+=sdata[tid+256];} __syncthreads();
}
if(blockSize>=256){
  if(tid<128){sdata[tid]+=sdata[tid+128];} __syncthreads();
}
if(blockSize>=128){
  if(tid<64){sdata[tid]+=sdata[tid+64];} __syncthreads();
}
if(tid<32){
  if(blockSize >= 64) sdata[tid] = sdata[tid+32];
  if(blockSize >= 32) sdata[tid] = sdata[tid+16];
  if(blockSize >= 16) sdata[tid] = sdata[tid+8];
  if(blockSize >=  8) sdata[tid] = sdata[tid+4];
  if(blockSize >=  4) sdata[tid] = sdata[tid+2];
  if(blockSize >=  2) sdata[tid] = sdata[tid+1];
}

GEMM¶

参考资料¶

深入浅出 GPU 优化系列：GEMM 优化（一） - 知乎 (zhihu.com)

SC'2010 Fast implementation of DGEMM on Fermi GPU¶

为了让计算单元充分利用，不让访存称为瓶颈。根据实际硬件参数，可以得到对分块大小的一个下界

\(\#\mathrm{CUDA}\times\mathrm{freq}\times DW\times 1/2(1/b_m + 1/b_n)<BW\)
- DW 表示元素字节数，如 double float，8Byte
同理根据 shard memory 带宽，可以得到\(r_x, r_y\)的不等式

根据 shared memory 大小，可以得到分块大小的一个上界 \((b_m*b_k + b_n*b_k)*DW < M_{shared}\) 根据 register file 的大小，得到 rx, ry 的上界 \((r_x+r_y+r_x*r_y)*{TRHEAD\_PER\_BLOCK} < 32768\)

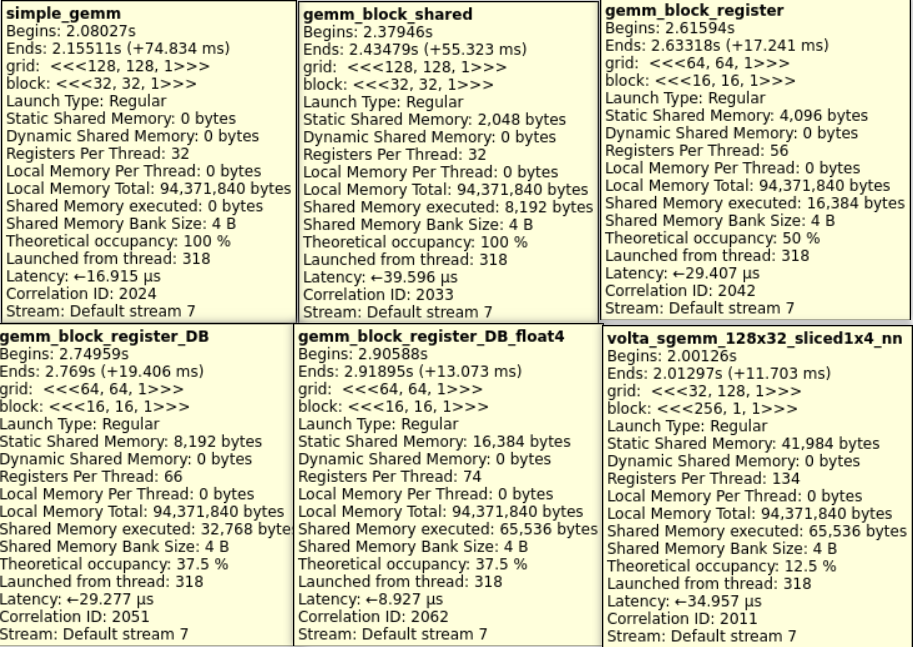
实践¶

simple
- C 中每个元素每个对应一个线程。
  - 由于一个块内线程数有上限，因此仍然需要划分块。
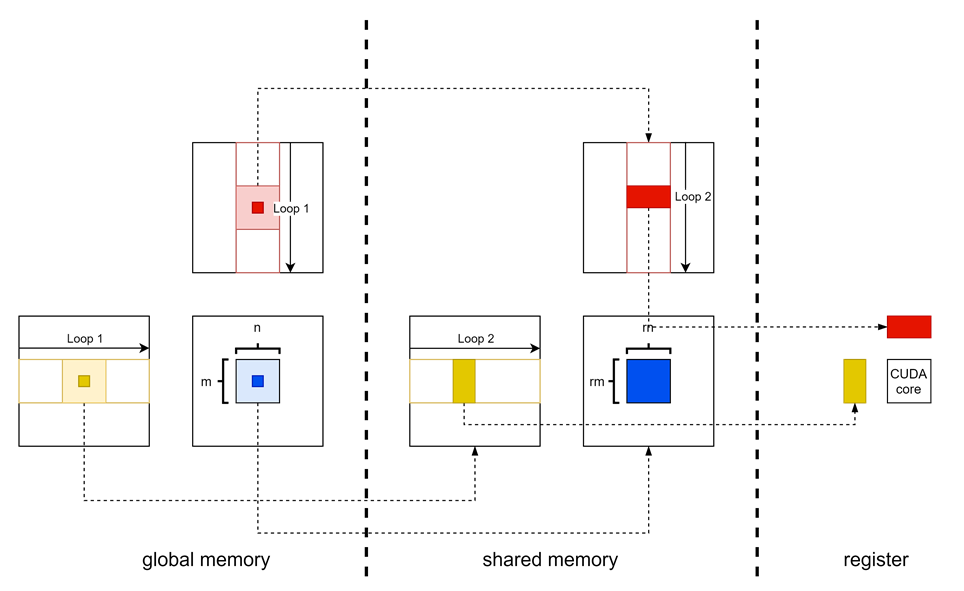
block shared memory
- 可以发现计算 C 中相邻元素时，会利用重复的行或列。因此可以考虑将若干线程组织成一个块，共享一部分数据。刚好对应硬件的 SMEM。