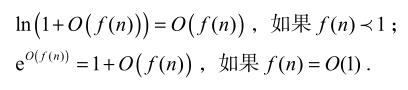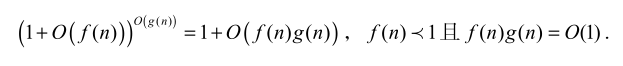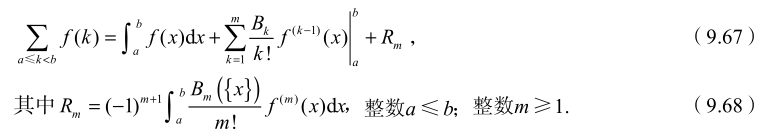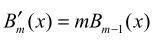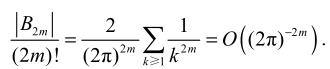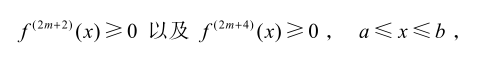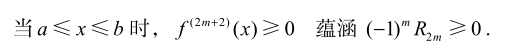具体数学
具体数学公式小册子¶
推广一个自己的 github 仓库,期望共同完善。 阅读具体数学电子书籍时,由于经常需要查看某个编号的公式因此产生了这个项目,用于阅读时查阅公式 https://github.com/TheRainstorm/concrete_math_formulas
成套方法¶
在具体数学 (Concrete Mathematics) 课本中,在解约瑟夫递推方程时,第一次介绍了成套方法 (repertoire method)。之后也使用这种方式求解各种递推方程。相信很多人第一次看到这种方法时都会感觉到不可思议——还能这样?虽然每一步都能看懂,但是就是不知道这种方法是怎么想到的。在查阅了一点资料后,我对该方法有了更多的认识。先说明一点,该方法并不是一种万能方法,实际上要求问题要有线性结构。
参考:linear algebra - Mathematical explanation for the Repertoire Method - Mathematics Stack Exchange
- 主要思路是由特解构造一般解
- 简单的,以$$ x_n = a_n + x_{n-1}$$ 则对于 $$ z_n = \alpha a_n + \beta b_n + z_{n-1} $$ \(z_n\)的解为 $$ z_n = \alpha x_n + \beta y_n $$
- 推广后
对于以下求解\(x_n\)的问题
$$
x_n = f(n) + g(x_{n-1}, x_{n-2}, ..., x_1)
$$
其中\(g()\)是一个线性函数
构造出\(k\)个 repertoire(可以理解为特解) $$ x_n^l = f^l(n) + g(x^l_{n-1}, x^l_{n-2}, ..., x^l_1), 0\le l \lt k $$ 使得可以 $$ f(n) = \sum_{0\le l \lt k} \lambda_l f^l(n) $$ 从而 $$ x_n = \sum_{0\le l \lt k} \lambda_l x_n^l $$ - 对于原本的约瑟夫问题 $$ \left{\begin{array}{l} f(1) = a \ f(2n) = 2f(n) + b\ f(2n+1) = 2f(n) + c\ \end{array}\right. $$ 有 $$ f(n) = aA(n) + bB(n) + cC(n) $$ 因此,对于不同的 a, b, c 的线性组合,可以得到新的递推方程,其解也是不同特解 f(n) 的线性组合
应用¶
求解三数取中位数版本的快速排序,比较次数。递推公式很复杂,但是却可以应用成套方法:linear algebra - Mathematical explanation for the Repertoire Method - Mathematics Stack Exchange $$ x_{n}=n+1+\frac{1}{\left(\begin{array}{c} n \ 3 \end{array}\right)} \sum_{1 \leq k \leq n}(k-1)(n-k)\left(x_{k-1}+x_{n-k}\right) $$
测试 MathJax 和 KaTex¶
block¶
aligned¶
$$
\begin{align*}
\sum_{k=1}^{n} k2^k &= \sum_{1\le j\le k \le n} 2^k \\
&= \sum_{1\le j\le n} \sum_{j \le k \le n} 2^k && \text{//考虑j, k 范围构成的三角形}\\
&= \sum_{1\le j\le n} 2^j(2^{n-j+1} - 1) \\
&= \sum_{1\le j\le n} 2^{n+1} - 2^j \\
&= n2^{n+1} - 2(2^n - 1) \\
&= (n-1)2^{n+1}+2 \\
\end{align*}
$$
math in list¶
- list $$ z_n = \alpha a_n + \beta b_n + z_{n-1} $$
- list
$$ z_n = \alpha a_n + \beta b_n + z_{n-1} $$
- list $$ z_n = \alpha a_n + \beta b_n + z_{n-1} $$
- list $$ z_n = \alpha a_n + \beta b_n + z_{n-1} $$
和式¶
- 将一重和式变为二重和式的例子 $$ \begin{align} \sum_{k=1}^{n} k2^k &= \sum_{1\le j\le k \le n} 2^k \ &= \sum_{1\le j\le n} \sum_{j \le k \le n} 2^k && \text{//考虑 j, k 范围构成的三角形}\ &= \sum_{1\le j\le n} 2j(2 - 1) \ &= \sum_{1\le j\le n} 2^{n+1} - 2^j \ &= n2^{n+1} - 2(2^n - 1) \ &= (n-1)2^{n+1}+2 \ \end{align} $$ p39 $$ \begin{aligned} S_{n} &=\sum_{1 \leqslant k \leqslant n} k^{2}=\sum_{1 \leqslant j \leqslant k \leqslant n} k \ &=\sum_{1 \leqslant j \leqslant n} \sum_{j \leqslant k \leqslant n} k \ &=\sum_{1 \leqslant j \leqslant n}\left(\frac{j+n}{2}\right)(n-j+1) \ &=\frac{1}{2} \sum_{1 \leqslant j \leqslant n}\left(n(n+1)+j-j^{2}\right) \ &=\frac{1}{2} n^{2}(n+1)+\frac{1}{4} n(n+1)-\frac{1}{2} S_{n}=\frac{1}{2} n\left(n+\frac{1}{2}\right)(n+1)-\frac{1}{2} S_{n} \end{aligned} $$
-
p33 $$ S_{n}=\sum_{1 \leqslant j<k \leqslant n} \frac{1}{k-j} $$ 无论是先对 j 求和,还是先对 k 求和,最终都只能导出\(S_n = \sum_{1\le j<n} H_j\)
先用 k 替换 k-j,然后对 j 先求和可以导出\(S_n = nH_n - n\)
- aa
- a $$ \sum_{\substack{j \in J \ k \in K}} a_{j} b_{k}=\left(\sum_{j \in J} a_{j}\right)\left(\sum_{k \in K} b_{k}\right) $$
- b $$ S \nabla=\sum_{1 \leqslant j \leqslant k \leqslant n} a_{j} a_{k}=\frac{1}{2}\left(\left(\sum_{k=1}^{n} a_{k}\right){2}+\sum_{k=1}\right) $$} a_{k}^{2
- c $$ \left(\sum_{k=1}^{n} a_{k}\right)\left(\sum_{k=1}^{n} b_{k}\right)=n \sum_{k=1}^{n} a_{k} b_{k}-\sum_{1 \leqslant j<k \leqslant n}\left(a_{k}-a_{j}\right)\left(b_{k}-b_{j}\right) $$
差分¶
-
微分 vs 差分 $$ Df(x) = \lim_{h\rightarrow0}{f(x+h) - f(x) \over h} $$
\[ \Delta f(x) = f(x+1) - f(x) \]
- 有限定积分含义 $$ \sum_a^b f(x)\delta x = \sum_{a\le x<b}f(x) = g(x)|_a^b $$ 其中 $$ \Delta g(x) = f(x) $$
- 下降幂的推广 $$ \begin{array}\ x^2 &= x(x-1) \ x^1 &= x \ x^0 &= 1 \ x^{-1} &= {1 \over x+1} \ x^{-2} &= \frac{1}{(x+1)(x+2)} \end{array} $$ 满足指数加法 $$ x{\underline{m+n}}=x $$}}(x-m)^{\underline{n}
-
几个函数积分
下降幂 $$ \sum x^{\underline{m}}\delta x = \left{\begin{array} \ {x^{\underline{m+1}} \over m+1} &m \ne -1 \ H(x) &m=-1 \ \end{array}\right. $$ 指数 $$ \sum c^x\delta x = {c^x \over c-1} $$
- 分布积分 $$ \sum u\Delta v = uv - \sum E v \Delta u $$ 其中 E 为移位算子,\(Ef(x) = f(x+1)\)
- 分布积分例子 $$ \begin{aligned} \sum x H_{x} \delta x &=\frac{x^{2}}{2} H_{x}-\sum \frac{(x+1)^{\underline{2}}}{2} x^{\underline{-1}} \delta x \ &=\frac{x^{2}}{2} H_{x}-\frac{1}{2} \sum x \delta x \ &=\frac{x^{2}}{2} H_{x}-\frac{x^{2}}{4}+C \end{aligned} $$
底和顶函数、模¶
-
a $$ n=\left\lfloor\frac{n}{m}\right\rfloor+\left\lfloor\frac{n+1}{m}\right\rfloor+\cdots+\left\lfloor\frac{n+m-1}{m}\right\rfloor $$
\[ \lfloor m x\rfloor=\lfloor x\rfloor+\left\lfloor x+\frac{1}{m}\right\rfloor+\cdots+\left\lfloor x+\frac{m-1}{m}\right\rfloor \]
-
b $$ \sum_{0 \leq k<m}\left\lfloor\frac{n k+x}{m}\right\rfloor=d\left\lfloor\frac{x}{d}\right\rfloor+\frac{m-1}{2} n+\frac{d-m}{2} $$
证明: $$ \sum_{0 \leq k<m} \left\lfloor\frac{n k}{m}\right\rfloor + \sum_{0 \leq k<m} \left\lfloor\frac{r_k + x}{m}\right\rfloor $$
同余¶
同余除法¶
同余是一种等价关系(自反、对称、传递)。满足加减乘,在某些条件下满足同余除法 $$ ad \equiv bd (\mod m) \ \Leftrightarrow a \equiv b (\mod m) \ 其中,(d, m)=1 $$ 证明时,一种简单的方法是等号两边同时乘与\(d'\),即 d 的逆元,\(dd'\equiv1 (\mod m)\)
中国剩余定理¶
特例 $$ \left{\begin{array}{l} x \equiv b \mod m \ x \equiv b \mod n \end{array}\right. \quad \Leftrightarrow x \equiv b \mod mn \
其中 (m, n)=1 $$ 一般情况,对于以下同余方程,可以找到其解\(x \equiv x_0 \mod mn\) $$ \left{\begin{array}{l} x \equiv a \mod m \ x \equiv b \mod n \end{array}\right. \quad 其中 (m, n)=1 $$
剩余系 & 独立剩余¶
剩余系 (residues number system): $$ res(x) = (x \bmod m_1, x \bmod m_2, ..., x \bmod m_r), \quad (m_i, m_j) = 1, m=m_1\cdot m_2 \dots m_r $$ 逆过程,知道了 x 在不同分量上的信息后,可以确定\(x \bmod m\)。(如果还知道 x 的范围,那么就能确定 x 的值)
如二维情况:可以先求解\((1, 0) = a, (0, 1)=b\),则\((x, y) = ax + by \mod m\)
若\(m_1 m_1' + m_2 m_2' = 1\),则\(a = m_2 m_2', b= m_1 m_1'\)
使用¶
\(x^2 \equiv 1 \mod m\)有多少解?
原方程等价于对任意\(m_p > 0\) $$ x^2 \equiv 1 \mod p^{m_p} $$ 因此,问题转化为在 m 的不同分量上进行求解 x,求解完后便可得到 x 的剩余系。
而对于该方程,当 p 不为 2 时,仅有两个解\(x = \pm1\)
当 p=2 时,有 4 个解\(x = \pm1, 1 \pm p^{m_p - 1}\)
x 在不同分量上的可能性的乘积即是所有可能
一些定理¶
费马小定理¶
\(n^p \equiv n \mod p\)或\(n^{p-1} \equiv 1 \mod p, p \nmid n\)
威尔逊定理¶
\((p-1)! \equiv -1 \mod p\)
关键在于 1, 2, ..., p-1 的数中
- \(nn' \equiv 1\)总存在
- \(x^2 \equiv 1\),仅当 x 为 1, p-1 时
因此 2, ... p-2 中两两互逆,剩余 1 和 p-1 和自己互逆
\(\varphi\)函数和\(\mu\)函数¶
欧拉函数¶
欧拉函数\(\varphi(n)\):1, 2, ... n-1 中和 n 互素的数的个数。另外\(\varphi(1) = 1\)
积性¶
欧拉函数是积性 (multiplicative) 的:
\(\varphi(mn) = \varphi(m) \varphi(n), 其中 (m,n)=1\)
原因:\((n, m) = 1 \Leftrightarrow (n, m_1) = 1, (n, m_2) = 1\)
积性一般定义: $$ \begin{array}{l} f(1) &= 1 \ f(m_1 m_2) &= f(m_1) f(m_2), m_1 \perp m_2 \end{array} $$ 积性引理
\(g(m) = \sum_{d|m} f(d)\)是积性的 \(\Leftrightarrow\) 那么 f(m) 也是积性的
从右往左很容易,从左往右可以使用数学归纳法。\(g(m_1m_2) = g(m_1)g(m_2)= \sum_{d_1|m_1} \sum_{d_2|m_2} f(d_1 d_2) = \sum_{d_1|m_1} \sum_{d_2|m_2} f(d_1)f(d_2) + f(m_1m_2) - f(m_1)f(m_2)\)(其中讨论了 d1 = m_1, d2=m2 的情况)
应用
因为欧拉函数是积性的,因此只需要考虑\(m=p^k\)的情况(对所有的积性函数都是这个套路)
易得\(\varphi(p^k) = p^k - p^{k-1} = p^k(1-1/p)\)
最后得:\(\varphi(m)=m\prod_{p} (1 - 1/p)\)
莫比乌斯函数¶
\(\mu(m)\)由下式确定(实质是一个递归式,后一项需要由前面的算出)
\(\sum_{d|m} \mu(d) = [m=1]\)
由前面的积性引理,可知莫比乌斯函数也是一个积性函数。故只需要考虑素数情况
\(\mu(p^k) = \left\{\begin{array}. -1 \quad k = 1\\ 0 \quad k> 1\end{array}\right.\)
所以 $$ \mu(m) = \left{\begin{array}. (-1)^r & m = p_1p_2...p_r\ 0 & \exists m_p > 1 \end{array}\right. $$
反演定理¶
反演定理(inversion principle) $$ g(m) = \sum_{d|m} f(d) \Leftrightarrow f(m) = \sum_{d|m}\mu(d)g(m/d) $$ 证明 $$ \begin{align} \sum_{d|m}\mu(d)g(m/d) &= \sum_{d|m}g(d)\mu(m/d)\ & = \sum_{d|m}\mu(m/d)\sum_{k|d} f(k) \ 令 d = kl \ & = \sum_{k|m}\sum_{l | m/k} f(k)\mu(m/kl) \ & = \sum_{k|m}fk \ & = f(m) \end{align} $$
应用
有欧拉函数和\(\sum_{d|m} \varphi(d) = m, 1\le d \le m\)
说明:考虑写出 1/m, 2/m, ... m/m,的所有分数,经过化简后,不同分母的分数个数和正好是 m。
因此由反演定理,可得欧拉函数的另一种表示
\(\varphi(m) = \sum_{d|m}\mu(d)m/d\),其中有大量 0 项。可以仅考虑\(d | p_1p_2...p_r\)的情况,共有 2^r 个非零项。对应\(m\prod_{p|m} (1 - 1/p)\)展开后的每一项(刚好 2^r) 项。
更强的反演定理 $$ g(x)=\sum_{d \geqslant 1} f(x / d) \Leftrightarrow f(x)=\sum_{d \geqslant 1} \mu(d) g(x / d) . $$ 这个反演法则对所有满足 \(\sum_{k, d \geqslant}|f(x / k d)|<\infty\) 的函数 \(f\) 都成立
证明变换有点巧妙,其中的 m 替换没看懂有什么好的证明方法 $$ \begin{aligned} \sum_{d \geqslant 1} \mu(d) g(x / d) &=\sum_{d \geqslant 1} \mu(d) \sum_{k \geqslant 1} f(x / k d) \ &=\sum_{m \geqslant 1} f(x / m) \sum_{d, k \geqslant 1} \mud \ &=\sum_{m \geqslant 1} f(x / m) \sum_{d \backslash m} \mu(d)=\sum_{m \geqslant 1} fx / m=f(x) . \end{aligned} $$
\(\Phi 函数\)¶
\(\Phi(x) = \sum_{1\le k\le x}\varphi(k)\),表示分母小于 x 的所有最简分数个数。
有 $$ \sum_{d\ge1}\Phi(x/d) = 1/2\lfloor x \rfloor \lfloor x+1 \rfloor $$ 证明:计数
对分子分母小于 x 的所有分数进行计数,即\(S = \{n/m| 1\le n,m \le \lfloor x \rfloor\}\),易知\(\# S = 右式\)
而 S 中的分数可以按照\(gcd(m, n) = d\)进行分类,其中每一类的个数即是\(\Phi(x/d)\)
珠子项链¶
有 n 种颜色的珠子,将其串成长度 m 的圆形项链,有多少种方法。 $$ \begin{aligned} m N(m, n) &=\sum_{a_{0}, \cdots, a_{m-1} \in S_{n}} \sum_{0 \leq k<m}\left[a_{0} \cdots a_{m-1}=a_{k} \cdots a_{m-1} a_{0} \cdots a_{k-1}\right] \ &=\sum_{0 \leq k<m} \sum_{a_{0}, \cdots, a_{m-1} \in S_{n}}\left[a_{0} \cdots a_{m-1}=a_{k} \cdots a_{m-1} a_{0} \cdots a_{k-1}\right] \
& = \sum_{0\le k <m} n^{gcd(k, m)} \end{aligned} $$ 一步巧妙的变换 $$ \begin{aligned} N(m, n) &=\frac{1}{m} \sum_{d \backslash m} n^{d} \sum_{0 \leqslant k<m}[d=\operatorname{gcd}(k, m)] \ \end{aligned} $$ 问题变成了,\(0\le k < m\)中有多少使得 gcd(k, m)=d 的 k(已知 d|m)。可知为\(\varphi(m/d)\)
麦克马洪公式 $$ N(m, n) = \frac{1}{m} \sum_{d \backslash m} n^{d}\varphi(m/d) $$ 其中可得,该公式并不明显,书上也给出了 1 页半的证明。 $$ \sum_{d \backslash m} \varphi(d) n^{m / d} \equiv 0(\bmod m) $$
一些变换¶
5 二项式系数¶
定义 $$ {r \choose k} = \left{\begin{array}\ {r^{\underline k} \over k!} &k\ge0\ 0 &k<0\end{array}\right. $$
- r 可以为实数
- \(r \choose k\)可以看作 r 的一个 k 次多项式
- 一般情况使用阶层改写 $$ {n \choose k} = \frac{n!}{k!(n-k)!} $$
对称性 $$ {n \choose k} = {n \choose n-k} $$ 对\(n \le 0\)不成立,(貌似对 n 非整数也不成立)
组合解释
吸收 (absorption) 恒等式¶
组合解释
记忆:左右关于 r 齐次 $$ k{r \choose k} = r{r-1 \choose k-1} $$ 伴随恒等式(保持下指标不变) $$ (r-k){r \choose k} = r{r-1 \choose k} $$ 上式可以看作是 r 的 k 次多项式的恒等式,(推导中 r 必须是正整数,但实际上对所有 r 都成立)书上称为多项式推理法 (polynomial argument)
加法公式¶
记忆:直角坐标系版的杨辉三角形中,一个数等于其上方和左上方的数的和 $$ {r \choose k} = {r-1 \choose k-1} + {r-1 \choose k} $$
- 组合解释:分类讨论元素 n 是否被选中
- 可以按照定义,也可以通过两个吸收恒等式相加得到
- 加法公式可以看作是一个递推式
推论,关于上指标求和(summation on the upper index),其中上下指标相差为一个定值的和也很重要 $$ \begin{align} \sum_{k=0}^{n} {k \choose m} &= \sum_{k=m}^{n} {k \choose k-m}\ &= \sum_{l=0}^{r} {m+l \choose l} &\text{\(r = n-m\)}\ &= {m+r+1 \choose r+1} \ &= {n+1 \choose m+1} \end{align} $$
- 组合解释:如果我们想要从一个有 1 + n 张票(标号从 0 直到 n)的集合中选取 m +1 张票,当选取的最大号码是数 k 时就有\(k \choose m\)种取法
- 和下降幂公式的联系(将下式两边除以 m!) $$ \sum_{0\le k \le n} k^{\underline m} = {(n+1)^{\underline{m+1}} \over m+1} $$
二项式定理¶
- binomial theorem $$ (x+y)^r = \sum_k {r \choose k} x^k y^{r-k} \text{整数\(r\ge0\)或者\(|x/y|<1\)} $$
- r 不是非负整数时 $$ (1+z)^r = \sum_k {r \choose k} z^k, |z|<1 $$
- 使用泰勒级数在 0 处展开,可以证明该公式(组合解释只说明了 r 是非负整数的情况)
反转上指标¶
negating the upper index $$ {r \choose k} = (-1)^k {k-r-1 \choose k} \ r^{\underline{k}} = r(r-1)...(r-k+1) =\ (-1)^k (-r)(1-r)..(k-1-r) = (-1)^k (k-1-r)^{\underline{k}}\
$$
二项式系数求和¶
二项式系数的恒等式非常多,记不完的。见表 5-3 二项式系数乘积和。
其中重要的,见书上 p143 页表 5-4 的 12 个最重要的二项式系数恒等式
在证明一些恒等式时,加法公式和数学归纳法结合的很好
范德蒙卷积¶
组合解释:r+s 集合分为 r 和 s 两类
最重要的 12 个恒等式¶

基本练习¶
问题 1:比值的和式 $$ \begin{align} \sum_{k=0}^{m} {m \choose k}/{n \choose k} & = \sum_{k \ge 0} {n - k \choose m - k}/{n \choose m}\ &= 1/{n \choose m}\sum_{k \le m} {n - m + k \choose k}\ &= {n+1 \choose m} /{n \choose m} \ &= \frac{n+1}{n+1-m} \end{align} $$ 问题 2: $$ \begin{align} \sum_{k=0}^{n} k{m -k - 1 \choose m - n - 1} & = \sum_{k=0}^{n} (m - (m-k)){m -k - 1 \choose m - n - 1}\ &= \sum_{k=0}^{n} m{m -k - 1 \choose m - n - 1} - \sum_{k=0}^{n} (m-k){m -k - 1 \choose m - n - 1}\ \end{align} $$ 问题 6:
\(n \ge 0\) $$ \begin{align} \sum_{k\ge0} {n+k \choose 2k}{2k \choose k}\frac{(-1)^k}{k+1} & = \sum_{k\ge0}{n+k \choose k}{n \choose k}\frac{(-1)^k}{k+1}\ &= \sum_{k\ge0}{n+k \choose k}{n+1 \choose k+1}\frac{(-1)^k}{n+1}\ \end{align} $$ 对称性 $$ \begin{align} \sum_{k\ge0}{n+k \choose k}{n+1 \choose k+1}\frac{(-1)^k}{n+1} &= \sum_{k}{n+k \choose k}{n+1 \choose k+1}\frac{(-1)^k}{n+1}\ &= \sum_{k}{n+k \choose n}{n+1 \choose k+1}\frac{(-1)^k}{n+1}\ &= 0 \end{align} $$ 从\({n+k \choose k}变为{n+k \choose n}\),当\(k<-n\)时,会从一个零值变为一个非零值。但是由于另一项\({n+1 \choose k+1}\)在\(k<-n\)时为 0,除了\(n=0\)时\(k=-1\)的情况为 1,因此答案为\(0 - {-1 \choose 0}(-1)^{-1} = 1\)
或则直接利用反转上指标
处理的技巧¶
取一半¶
可以知道,当上指标非整数时,取值很特别。
高阶差分¶
即 $$ \sum_{k} {n \choose k}(-1)^{n-k}f(x+k) = \Delta^{n}f(x) $$ 或\(\sum_{0}^{n} {n \choose k}(-1)^{k}f(x+k) = (-1)^n \Delta^{n}f(x)\)
或\(\sum_{0}^{n} {n \choose k}(-1)^{k}f(k) = (-1)^n \Delta^{n}f(0)\)
牛顿级数¶
假如 f(x) 是一个 d 次多项式,则 f(x) 可以写成下降幂的和式 $$ f(x) = b_dx^{\underline{d}} + b_{d-1}x{\underline{d-1}}+...+b_1x $$ 更进一步,可以写成二项式系数的和 $$ f(x) = c_d{x \choose d} + c_{d-1}{x \choose d-1}+...+c_{0}{x \choose 0} $$}} + b_0x^{\underline{0}
可以通过计算高阶差分,求解这些系数。类似于泰勒展开。 $$ \Delta^{n} {x \choose d} = {x \choose d-n} $$
比如要计算\(f(x) = x^3\)的牛顿级数 $$ f(0) = 0, f(1) = 1, f(2) = 8, f(3) = 27\ \Delta f(0) = 1, \Delta f(1) = 7, \Delta f(2) = 19,\ \Delta^2 f(0) = 6, \Delta f(1) = 12,\ \Delta^3 f(0) = 6, $$ 因此\(x^3 = 6{x \choose 3} + 6{x \choose 2} + {x \choose 1}\)
因此\(\sum_{k=0}^{n-1} k^3 = 6{n \choose 4} + 6{n \choose 3} + {n \choose 2}\)
反演¶
书本 p159 处\(f(k) = {r - sk \choose n} = \frac{1}{n!}(-n)^n...\)中的\((-n)^n\)应该是\((-1)^n\),印刷错误。
生成函数¶
卷积
生成函数计算
B_2(z) 的系数为卡塔兰数 Catalan number C_n
广义二项级数和广义指数级数¶
一般卷积公式¶
- 有(5.60)
如 $$ (t k)^{\underline{k-1}}\frac{1}{k!} = (tk+1)^{\underline{k}}/(tk+1)\frac{1}{k!} = C_k^{(t, 1)} $$ 之后会证明: $$ [z^k]\mathcal{B}_t(z) = [z{k-1}]\mathcal{B}_t(z)t $$
- 又有 (5.61)
构造生成函数\(\mathcal{B}_{t}(z)^{r} \frac{\mathcal{B}_{t}(z)^{s}}{1-t+t \mathcal{B}_{t}(z)^{-1}}\),得一般卷积公式 (5.62): $$ \begin{equation} \sum_{k}{t k+r \choose k}{t n-t k+s \choose n-k} \frac{r}{t k+r}={t n+r+s \choose n} \end{equation} $$
特殊级数\(\sqrt{1\pm4z}\)¶
B_2 封闭形式 (5.68)(书上没有证明)¶
证明 (5.72) $$ \begin{equation} \frac{\mathcal{B}{2}(z)^{r}}{\sqrt{1-4 z}}=\sum \end{equation} $$ 证明:}{2 k+r \choose k} z^{k
有(类似于上面证明) $$ \frac{1}{\sqrt{1-4z}} = \sum_{k}{2k \choose k} z^k $$ 构造生成函数\(\mathcal{B}_{2}(z)^{r} \frac{1}{\sqrt{1-4z}}\),再由一般卷积公式可得。
类似可得 (5.73) $$ \begin{equation} \frac{\mathcal{B}{-1}(z)^{r+1}}{\sqrt{1+4 z}}=\sum \end{equation} $$ }{r-k \choose k} z^{k证明 (5.74) $$ \begin{equation} \sum_{k \leqslant n}{n-k \choose k} z^{k}=\frac{1}{\sqrt{1+4 z}}\left(\left(\frac{1+\sqrt{1+4 z}}{2}\right)^{n+1}-\left(\frac{1-\sqrt{1+4 z}}{2}\right)^{n+1}\right) \text {, 整数 } n \geqslant 0 \end{equation} $$ 证明:
可证明 k>n 时 $$ [zk]\frac{(-z)}\mathcal{B{2}(-z)^{n+1}}{\sqrt{1+4 z}} = {n-k \choose k} $$ ,故 $$ \begin{equation} \frac{\mathcal{B}(z){n+1}-(-z)} \mathcal{B{2}(-z)^{n+1}}{\sqrt{1+4 z}}=\sum n-k \ k \end{array}\right) z^{k} \end{equation} $$}\left(\begin{array}{c
超几何函数¶
- 带有 m 个上参数,n 个下参数。对于参数个数为 0 的情况,可以上下添加一个常数 1 而不会影响(参数个数仍然是 0 个)。
- 如 m=1, n=0 的情况对应
- m=0, n=1 为修正贝塞尔函数(modified Bessel function)
- m=1, n=1 为合流超几何级数(confluent hypergeometric series)
- 而 m=2, n=1 被称为高斯超几何函数
今天,在许多大学 的物理学、工程学甚 至数学专业的学生 所学习的函数中,即 使不是 100% ,也必定 有 95% 的函数被这单 个的符号 F ( a , b ; c ; x ) 所涵盖.” —— W.W. 索耶 [318]
有非常多的性质,如 $$ \begin{align} \ln (1+z)=z F\left(\begin{array}{c} 1,1 \ 2 \end{array} \mid-z\right) &=z \sum_{k \geqslant 0} \frac{k ! k !}{(k+1) !} \frac{(-z)^{k}}{k !} \ &=z-\frac{z{2}}{2}+\frac{z+\cdots \end{align}}{3}-\frac{z^{4}}{4} $$
超几何函数表示¶
超几何级数恰好就是首项为 1 且项的比值 t k+1 /t k 是 k 的有理函数的那些级数 $$ \begin{equation} \begin{aligned} \frac{t_{k+1}}{t_{k}} &=\frac{a_{1}^{\overline{k+1}} \cdots a_{m}{\overline{k+1}}}{a_{1}}} \cdots a_{m}^{\bar{k}}} \frac{b_{1}^{\bar{k}} \cdots b_{n{\bar{k}}}{b_{1} \frac{z}} \cdots b_{n}^{\overline{k+1}}} \frac{k !}{(k+1) !{k+1}}{z \ &=\frac{\left(k+a_{1}\right) \ldots\left(k+a_{m}\right) z}{\left(k+b_{1}\right) \ldots\left(k+b_{n}\right)(k+1)} \end{aligned} \end{equation} $$}
平行求和表示为超几何函数¶
平行求和: $$ \sum_{k\le n} {r+k \choose k} = \sum_{k\ge 0}{r +n -k \choose n-k} = {r+n+1 \choose n} $$ 而 $$ \frac{t_{k+1}}{t_k}= \frac{(k+1)(k-n)(1)}{(k-n-r)(k+1)} \ t_0 = {r+n \choose n} $$ 故 $$ {r+n \choose n} F(1, -n; -n-r; 1) = {r+n+1 \choose n} $$ 即 $$ F(1, -n; -n-r; 1)=\frac{r+n+1}{r+1} $$ 类似的另一个求和也可以表示为超几何函数: $$ \sum_{k\le m} {r \choose k}(-1)^k = F(1, -m; -m+r+1; 1) $$ 这两个超几何级数均 m=1, n=1,可以相互推出。
两个限制¶
-
下参数不能为 0 或者负整数
原来我们是对整 数 r 证明了这些恒等 式,并用多项式推理 法指出它们在一般 情形也成立. 现在我 们是首先证明它们 对无理数 r 成立,并 利用极限方法指出 它 们 对 整 数 也 成立
- 使用阶乘将\({r+n-k \choose n-k}\)展开了,而阶乘原本对负整数时没定义。
阶乘推广¶
欧拉¶
所有复数 z $$ \frac{1}{z!} = \lim_{n\rightarrow \infin} {n+z \choose n}n^{-z} $$
\(\Gamma 函数\)¶
通过 $$ z! = z(z-1)! $$ 将该定义延拓到\(C - Z^-\)(除了负整数外的复数)
阶乘和伽马函数可以相互替换使用。 $$ \Gamma(z+1) = z!\ (-z)!\Gamma(z) = \frac{\pi}{\sin{\pi z}} $$ 广义阶乘幂 $$ z^{\underline{w}} = \frac{z!}{(z-w)!}\ z^{\bar{w}} = \frac{\Gamma(z+w)}{\Gamma(z)}\ $$ 二项式系数 $$ \left(\begin{array}{c} z \ w \end{array}\right)=\lim {\zeta \rightarrow z} \lim $$} \frac{\zeta !}{\omega !(\zeta-\omega) !
牛顿级数¶
范德蒙卷积¶
得 $$ \begin{equation} F\left(\begin{array}{c} a, b \ c \end{array} \mid 1\right)=\frac{\Gamma(c-a-b) \Gamma(c)}{\Gamma(c-a) \Gamma(c-b)} ; \text { 整数 } b \leqslant 0 \text {, 或者 } \mathfrak{c} c>\Re a+\Re b . \end{equation} $$ 特殊情形 $$ \begin{equation} F\left(\begin{array}{c} a,-n \ c \end{array} \mid 1\right)=\frac{(c-a){\bar{n}}}{c=\frac{(a-c)}}{\frac{n}{n}}}{(-c) n \geqslant 0 \end{equation} $$ 因此基本所有之前的求和公式,都可以用这条公式查表的方式得到。}}, \quad \text { 整数
求极限¶
已知有(见 p177) $$ (-1)^{n} \frac{(2 n) !}{n !}=\lim {b \rightarrow-2 n} \frac{(b / 2) !}{b !}=\lim $$ 因此} \frac{x !}{(2 x) !\(-6!/3!=\lim_{x->-3}x!/(2x)!\)
- 如果认为 (-3) = (-3)(-4)(-5)(-6)!,然后消掉就会得到错误答案
-
使用 (5.87) 将负变量阶乘和正的伽马函数联系起来
最后一步使用洛必达 $$ \lim_{r \to 0}\frac{(-n-r)!\Gamma(n+r)}{(-2n - 2r)!\Gamma(2n+2r)} = \lim_{r \to 0}\frac{\sin(2n+2r)\pi}{\sin(n+r)\pi} = 2(-1)^n $$ 得 $$ \lim_{x \to -n} \frac{x!}{(2x)!} = \lim_{r \to 0}\frac{(-n-r)!}{(-2n - 2r)!} = 2(-1)^n \frac{\Gamma(2n)}{\Gamma(n)} = (-1)^n\frac{(2n)!}{n!} $$
不同极限
由 (5.20)\(\sum_{k \leqslant m}{m+k \choose k} 2^{-k}=2^{m} \to \sum_{k\ge 0}{2m-k \choose m-k}2^k = 2^{2m}\)
应该表示为 $$ \begin{equation} \left(\begin{array}{c} 2 m \ m \end{array}\right) \lim {\varepsilon \rightarrow \infty} F\left(\begin{array}{c} 1,-m \ -2 m+\varepsilon \end{array} \mid 2\right)=2^{2 m} \end{equation} $$ 不同极限是不同的 $$ \begin{equation} \begin{aligned} \lim -1+\varepsilon,-3 \ -2+\varepsilon \end{array} \mid 1\right)=\lim } F\left(\begin{array}{c{\varepsilon \rightarrow 0}\left(1+\frac{(-1+\varepsilon)(-3)}{(-2+\varepsilon) 1 !}+\frac{(-1+\varepsilon)(\varepsilon)(-3)(-2)}{(-2+\varepsilon)(-1+\varepsilon) 2 !}\right.\ \left.+\frac{(-1+\varepsilon)(\varepsilon)(1+\varepsilon)(-3)(-2)(-1)}{(-2+\varepsilon)(-1+\varepsilon)(\varepsilon) 3 !}\right) \ =1-\frac{3}{2}+0+\frac{1}{2}=0 ; \ \lim -1,-3 \ -2+\varepsilon \end{array}\right) =\lim _{\varepsilon \rightarrow 0}\left(1+\frac{(-1)(-3)}{(-2+\varepsilon) 1 !}+0+0\right) \ =1-\frac{3}{2}+0+0=-\frac{1}{2} . \end{aligned} \end{equation} $$} F\left(\begin{array}{l
超几何变换¶
已知的超几何级数封闭形式是计算二项式系数和的有用工具。
而超几何变换研究如何将一个超几何级数变换成另一个类似但不同参数的超几何级数。
1797 年,J. F. 普法夫 [292] 发现了一个惊人的反射定律(reflection law) $$ \frac{1}{(1-z)^{a}} F\left(\begin{array}{c|c} a, b & -z \ c & 1-z \end{array}\right)=F\left(\left.\begin{array}{c} a, c-b \ c \end{array}\right| z\right) $$
微分方式得到 $$ \begin{equation} \begin{aligned} &\frac{d}{d z} F\left(\begin{array}{l} a_{1}, \cdots, a_{m} \ b_{1}, \cdots, b_{n} \end{array} \mid z\right)=\sum_{k \geqslant 1} \frac{a_{1}^{\bar{k}} \cdots a_{m}^{\bar{k}} z{k-1}}{b_{1}\ &=\sum_{k+1 \geqslant 1} \frac{a_{1}^{\overline{k+1}} \cdots a_{m}^{\overline{k+1}} z}} \cdots b_{n}^{\bar{k}}(k-1) !{k}}{b_{1}\ &=\sum_{k \geqslant 0} \frac{a_{1}\left(a_{1}+1\right)^{\bar{k}} \cdots a_{m}\left(a_{m}+1\right)^{\bar{k}} z}} \cdots b_{n}^{\overline{k+1}} k !{k}}{b_{1}\left(b_{1}+1\right)\ &=\frac{a_{1} \ldots a_{m}}{b_{1} \ldots b_{n}} F\left(\begin{array}{ll} a_{1}+1, \ldots, & a_{m}+1 \ b_{1}+1, \ldots, & b_{n}+1 \end{array} \mid z\right) \text {. } \end{aligned} \end{equation} $$}} \cdots b_{n}\left(b_{n}+1\right)^{\bar{k}} k !
另一个算子 $$ \vartheta = z\frac{d}{d z} $$
于是超几何函数满足微分方程,且是仅有的满足该微分方程常数项为 1 的形式幂级数 $$ \begin{equation} \mathrm{D}\left(\vartheta+b_{1}-1\right) \cdots\left(\vartheta+b_{n}-1\right) F=\left(\vartheta+a_{1}\right) \cdots\left(\vartheta+a_{m}\right) F, \end{equation} $$
F(a, b; c; z) 满足 $$ \begin{equation} z(1-z) F^{\prime \prime}(z)+(c-z(a+b+1)) F^{\prime}(z)-a b F(z)=0 \end{equation} $$ 微分理论的一个用途是发现并证明新的变换,如高斯恒等式,均满足相同的微分方程。 $$ \begin{equation} \left.\left.F\left(\begin{array}{c} 2 a, 2 b \ a+b+\frac{1}{2} \end{array}\right| z\right)=F\left(\begin{array}{c} a, b \ a+b+\frac{1}{2} \end{array}\right| 4 z(1-z)\right) \end{equation} $$
超几何级数对于理解二项式系数 和式提供了一个高水平的方法.更多的信息可以在 Bailey 所写的经典著作 [18] 以及其后由 Gasper 和 Rahman 合著的书 [141] 中找到
Gosper 算法 (求差分原函数)¶
1977 年,R. W. Gosper \({ }^{[154]}\) 发现了一个优美的方法,只要 \(f\) 和 \(g\) 属于称为超几何项的一般 函数类,就能用此法求出不定和式 \(\sum f(k) \delta k=g(k)+C\). 我们记 $$ F\left(\begin{array}{c} a_{1}, \cdots, a_{m} \ b_{1}, \cdots, b_{n} \end{array} \mid z\right){k}=\frac{a}^{\bar{k}} \cdots a_{m{\bar{k}}}{b_{1} $$ 为超几何级数 }} \cdots b_{n}^{\bar{k}}} \frac{z^{k}}{k !\(F\left(a_{1}, \cdots, a_{m} ; b_{1}, \cdots, b_{n} ; z\right)\) 的第 \(k\) 项。我们将把 \(\left.F\left(a_{1}, \cdots, a_{m} ; b_{1}, \cdots, b_{n} ; z\right)\right._{k}\) 看成是 \(k\) 而 不是 \(z\) 的一个函数。在许多情形下都表明,对给定的 \(a_{1}, \cdots, a_{m}, b_{1}, \cdots, b_{n}\) 以及 \(z\), 存在参数 \(c\), \(A_{1}, \cdots, A_{M}, B_{1}, \cdots, B_{N}\) 以及 \(Z\), 使得 $$ \sum F\left(\begin{array}{l} a_{1}, \cdots, a_{m} \ b_{1}, \cdots, b_{n} \end{array} \mid z\right){k} \delta k=c F\left(\begin{array}{l} A \ B_{1}, \cdots, B_{N} \end{array} \mid Z\right)_{k}+C . $$ 存在称为是可用超几何项求和的 (summable in hypergeometric terms )}, \cdots, A_{M
Gosper-Zeilberger 算法¶
\(t(n, k)\). 当 \(t(n, k)\) 给定时,Gosper-Zeilberger 算法可以总结如下: 0 置 \(l:=0\). ( 我们将寻求关于 \(n\) 的 \(l\) 阶递归式。) 1 令 \(\hat{t}(n, k)=\beta_{0}(n) t(n, k)+\cdots+\beta_{l}(n) t(n+l, k)\), 其中 \(\beta_{0}(n), \cdots, \beta_{l}(n)\) 是末知的函数。利用 \(t(n, k)\) 的性质寻求 \(\beta_{0}(n), \cdots, \beta_{l}(n)\) 的一个线性组合 \(p(n, k)\), 其系数是关于 \(n\) 和 \(k\) 的多项式,使 得 \(\hat{t}(n, k)\) 可以写成形式 \(p(n, k) \bar{t}(n, k)\), 其中 \(\bar{t}(n, k)\) 是关于 \(k\) 的超几何项。求多项式 \(\bar{p}(n, k)\) 、 \(q(n, k)\) 和 \(r(n, k)\), 使得 \(\bar{t}(n, k)\) 的项的比值表示成 \((5.128)\) 的形式,其中 \(q(n, k)\) 和 \(r(n, k)\) 满足 Gosper 条件 ( \(5.118)\). 置 \(\hat{p}(n, k)=p(n, k) \bar{p}(n, k)\). 2a 置 \(d_{Q}:=\operatorname{deg}(q-r), d_{R}:=\operatorname{deg}(q+r)\), 以及 $$ d:= \begin{cases}\operatorname{deg}(\hat{p})-d_{Q}, & d_{Q} \geqslant d_{R} \ \operatorname{deg}(\hat{p})-d_{R}+1, & d_{Q}<d_{R}\end{cases} $$ \(2 \mathrm{~b}\) 如果 \(d \geqslant 0\), 用 \((5.130)\) 定义 \(s(n, k)\), 并考虑关于 \(\alpha_{0}, \cdots, \alpha_{d}, \beta_{0}, \cdots, \beta_{l}\) 的诸个线性方 程,这些方程是在基本方程 ( 5.129) 中令 \(k\) 的幂的系数相等而得到的。如果这些方程有一个 使得 \(\beta_{0}, \cdots, \beta_{l}\) 不全为零的解,就转到第 4 步。如若不然,当 \(d_{Q}<d_{R}\) 且 \(-2 \lambda^{\prime} / \lambda\) 是一个大于 \(d\) 的 整数时 (其中 \(\lambda\) 是 \(q+r\) 中 \(k^{d_{R}}\) 的系数,而 \(\lambda^{\prime}\) 则是 \(q-r\) 中 \(k^{d_{R}-1}\) 的系数 ), 就置 \(d:=-2 \lambda^{\prime} / \lambda\) 并 重复第 \(2 \mathrm{~b}\) 步。 3 ( 项 \(\hat{t}(n, k)\) 不是超几何可求和的。) 将 \(l\) 增加 1 并回到第 1 步。 4(成功。) 置 \(T(n, k):=r(n, k) s(n, k) \bar{t}(n, k) / \bar{p}(n, k)\). 由该算法,就得到了 \(\hat{t}(n, k)=T(n\), \(k+1)-T(n, k) .\) 以后我们将要证明,只要 \(t(n, k)\) 属于称为正常项(proper term)的一个大类,这个算法 就能成功地终止。
6 特殊的数¶
-
第二类斯特林数(n 真子集 k)
$$ {n \brace k} = {n - 1 \brace k-1} + k{n-1 \brace k} $$
分别讨论第一个数:1)单独成为一个子集。2)从\({n-1 \brace k}\)中选择一个,有 k 种可能
- 特值
\({n \brace 2} = 2^{n-1}-1\)
- 特值
-
第一类 stirling 数(n 轮换 k)(在 n 子集 k 的每个子集上,乘上轮换的种类)
$$ {n \brack k} = {n - 1 \brack k-1} + (n-1){n-1 \brack k} $$
分别讨论第一个数:1)单独成为一个子集。2)从\({n-1 \brack k}\)中选择一个,\(t_1 +t_2+...+t_k = n-1\),加入\(t_i\)个元素的轮换时,种数为\(t_i{n-1 \brack k}\)
- 特殊值
\({n \brack 1} = (n-1)![n>0]\)
\({n \brack 2} = (n-1)!H_{n-1}[n>0]\)
- 特殊值
-
第一类 stirling 数和排列关系
-
一个排列对应一个轮换
- 排列\(\pi_1\pi_2...\pi_n\),表示将\(i \to \pi_i\)。从任一个元素出发,映射可以构成一个环。\(m_0 = m, m_k = \pi_{m_{k-1}}\)
- 一个轮换也可以构造一个排列,因此 $$ \sum_k {n \brack k} = n! $$
-
- stirling 数与下降幂 $$ x^n = \sum_k {n \brace k}x^{\underline{k}}, n\ge 0 $$
- 第二类 stirling 数与上升幂 $$ x^{\bar{n}} = \sum_k {n \brack k}x^k, n\ge 0 $$
-
对偶性
将 stirling 数对 n,k 不做任何限制后 (加上条件\({0 \brace k} = [k=0], {n\brace 0} = [n=0]\)) 可得 $$ {n \brack k} = {-k \brace -n} $$
欧拉数¶
- \({n }\)
7 生成函数¶
从之后来看,生成函数就是一个和式,包含关于研究问题的全部信息(贴瓷砖,概率分布。。。)
- 多米诺铺设,生成函数设置为所有铺设
- 忽略铺设方式(打散成零件),只考虑使用的行列多米诺数量
- 只考虑多米诺骨牌的数量:每一项系数为 3xn(或 2xn) 铺设在指定数量骨牌时的方式总数。
- 找硬币
- \([z^n]\frac{1}{1-z}\frac{1}{1-z^5}...\frac{1}{1-z^{50}}\)
- 书上通过转换成递归式求解
- 7.2 生成函数变换
- \(F(z) = \sum_n f_nz^n\),延拓到\(n \in Z, n<0 \to f_n=0\)
- 生成函数变换
- \(<\alpha f_n+\beta g_n> \to \alpha F(z) + \beta G(z)\)
- \(<0, 0,...,0_m, g_0, g_1,..>\) 或\(<g_{n-m}>\)
- \(<g_{n+m}>\)
- \(<ng_n>\),求导,\(zG'(z)\)
- \(n^2 g_n\)?
- \(<\frac{1}{n}g_n>\),求积分
- 卷积:\(F(z)G(z) = \sum_n(\sum_k g_k f_{n-k})z^n\)
- 生成函数求斐波那契数列
- \(f_0=0,f_1=1, f_n = f_{n-1} +f_{n-2}, n\ge 1\)
- \(f_n = f_{n-1} +f_{n-2} + [n=1], n\in Z\)
- \(G(z) = \frac{z}{1-z-z^2} = \frac{1}{\sqrt{5}}(\frac{1}{1-\alpha z} - \frac{1}{1-\beta z})\)
- 涉及到有理函数分解
- 7.3 解递推式
- 有理函数分解
- 相互递推数列 -> 二元一次方程组
- \(g_0 = 1, g_n = ng_{n-1}, n\ge 1\)
- \(G(z) = z^2G'(z) + zG(z) + 1\)
- 超几何级数,是满足 xxxx,且是唯一满足该方程且常数项为 1 的幂级数。
- 二重求和
- \(f_n = f_{n-1} + \sum_{k<n}f_k + 1\)
有理函数分解¶
-
特殊的生成函数
- aa
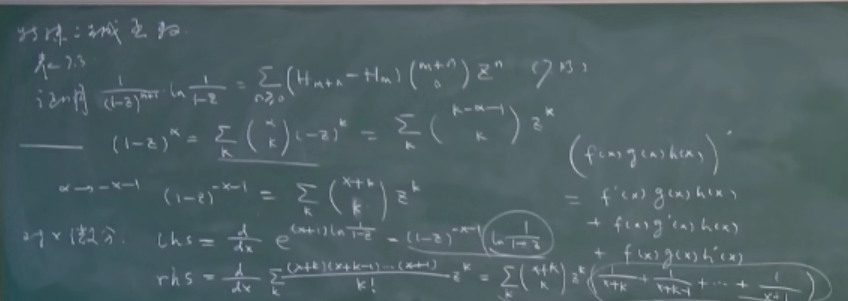
- aa
-
卷积
- bb
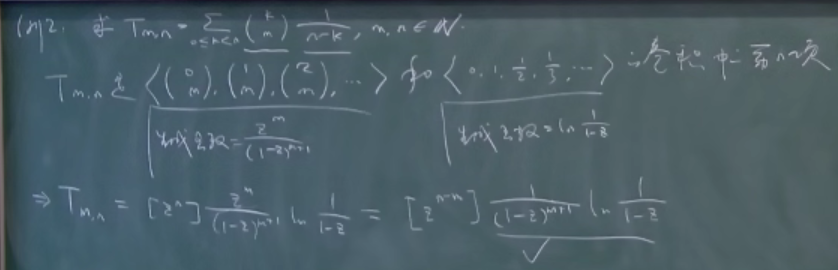
- aa
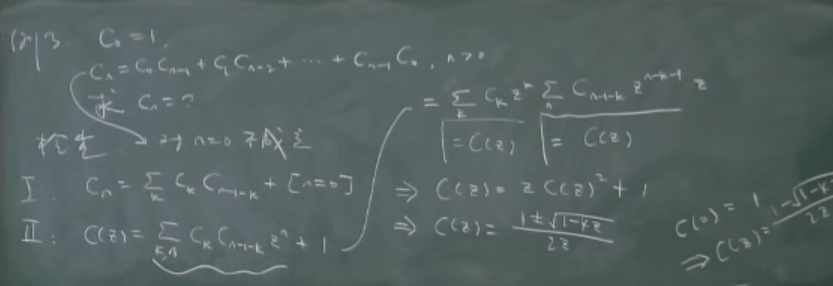
- bb
- 生成函数解生成树问题
- 卡塔兰数
卡塔兰数¶
证明 1:
-
ranny 引理
<\(x_1, x_2, ..., x_n\)>和为 1 的整数数列,则只有一个循环移位满足所有前部分和为正。
-
问题:从 0 走到 n 的走法
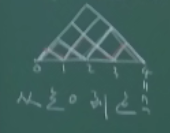
-
转换为:
- <\(x_1, x_2, ..., x_{2n}\)>, \(x_i = \pm 1\)
- \(\sum x_i = 0\)
- 部分和非负
- 构造
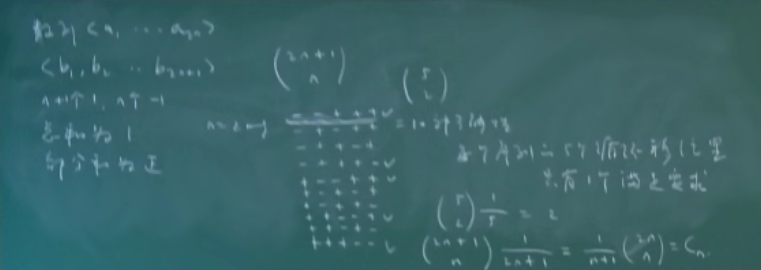
证明 2:
从 0 到 n,需要 n 次右上,n 次右下移动,有\({2n \choose n}\)种走法,减去其中出现部分和为负的情形
部分和为负的情形,可以构造一个反射的走法,\({2n \choose n-1}\)
\(C_n = {2n \choose n} - {2n \choose n-1}\)
证明 3:
引理:\(C_k^{(t, 1)} = (\sum_{k_1 + k_2 +...k_t = k-1}C_{k_1}^{(t,1)}...) + [k=0]\)
其中\(C_k^{(t, r)} = {tk + r \choose k} \frac{r}{tk + r}\)
证明
考虑由 1 和 (1-m) 构成的部分和为正的,总和为 1 的数列,称为 m-Ranmy 数列
考虑长度为 mn+1 的 m-Ranny 数列有多少个?
n 个 1-m, L 个 1,则长度 n+L = nm + 1
可说明(利用 Ranny 定理)
个数=\({nm + 1 \choose n}\frac{1}{nm+1} = C_n^{(m, 1)}\)
由引理,有:
G(z) 为\(<C_n^{(m, 1)}>\)的生成函数
\(G(z) = zG(z)^m +1\)
-
ranny 引理推广
\(x_1, x_2, ..., x_m\)序列和为 r,则其 m 个循环移位中有 r 个满足部分和为正。
指数生成函数¶
- 运算
- 求导:向左移
- 积分:向右移
- 乘积
8 离散概率¶
- 概率空间 (probability space)
- 基本事件 (elementary event) \(\omega \in \Omega\)
- 赋予基本事件一个概率\(Pr(\omega)\),满足非负,和为 1
- 概率分布 (probability distribution)
- 事件 (event)A 是概率空间的一个子集,概率定义为基本事件概率之和
- 随机变量(random variable),是定义在概率空间的基本事件\(\omega\)上的函数。比如骰子点数之和。
- \(X: \Omega \to set of value\)
- 随机变量使得我们不用研究整个概率空间,而只用研究我们关心的量。
- 独立 (independent)
- 事件独立?
- 随机变量独立:\(P(X=x, Y = y) = P(X=x) P(Y= y)\)
- 均值,期望值 (expected value):\(EX = \sum_{\omega}X(\omega)Pr(\omega) = \sum_{x \in X(\omega)}xPr(X=x)\)
- 中位数:\(P(X\le x)\ge 1/2\)且\(P(X\ge x) \ge 1/2\)
- 众数:\(P(X=x) \ge P(X=x'), \forall x' \in X(\Omega)\)
-
期望
- 可加(定义在同一个概率空间上,或独立):\(E(X+Y) = \sum_{\omega} (X(\omega) + Y(\omega))P(\omega) = EX + EY\)
- 乘积(独立): $$ \begin{aligned} &\mathrm{E}(X Y)=\sum_{\omega \in \Omega} X(\omega) Y(\omega) \cdot \operatorname{Pr}(\omega)\ &=\sum_{\substack{x \in X(\Omega) \ y \in Y(\Omega)}} x y \cdot \operatorname{Pr}(X=x \text { 且 } Y=y)\ &=\sum_{\substack{x \in X(\Omega) \ y \in Y(\Omega)}} x y \cdot \operatorname{Pr}(X=x) \operatorname{Pr}(Y=y) \end{aligned} $$
- 方差:\(DX = E(X^2) - (EX)^2\)
-
切比雪夫不等式:\(Pr((X-EX)^2 \ge \alpha)\le \frac{Var(X)}{\alpha}\)
- \(\operatorname{Pr}(|X-\mu| \geqslant c \sigma) \leqslant 1 / c^{2}\)
-
Markov 不等式:\(X\ge 0, \lambda>0\),有\(Pr(X\ge\lambda) \le \frac{EX}{\lambda}\)
- 直接导出切比雪夫不等式
- 还有:\(Pr(f(X)\ge f(\lambda)) \le \frac{Ef(X)}{f(\lambda)}\), f(x) > 0,单调增。
-
用样本估计期望,方差
- \(\hat{E} = \frac{1}{n}\sum_{k}X_k\)
- \(\hat{V} = \frac{1}{n-1}\sum_k (X_k - \hat{E})^2 = \frac{1}{n-1} \sum_k X_k^2 - \frac{1}{n(n-1)}(\sum_k E_k)^2\)
- 因为\(E\hat{V} = DX\)
- 考虑第 5 章的“足球胜利问题”,在该问题中有 n 顶帽子被抛向空中,有 k 个人得到自己的帽子。
- 可以在不计算概率分布的情况下,计算均值和方差
- \(F_n = F_{n,1}+F_{n,2}+\dots + F_{n,n}\),\(F_{n, k}\)表示第 k 个人是否拿到自己帽子
- \(EF_{n,k} = 1/n\), \(EF_n = 1\)
- $EF_n^2 = $
概率生成函数
- pgf 乘积对应随机变量和的分布
-
累积量(cumulant)
- 累积量独立可加
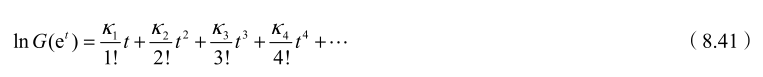
-
m 阶矩(m th moment)
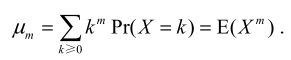
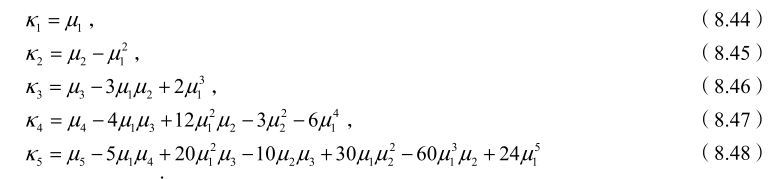
-
“阶乘矩”,(\(\alpha_m = G^{(m)}(1)\)
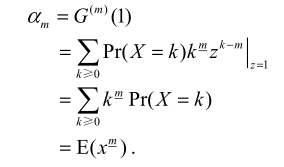
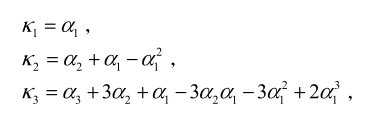
抛硬币
- 二项分布
-
负二项分布(和帕斯卡分布类似):抛出 n 次正面时,反面的次数
- 倒数生成函数,方便计算方差
- 有限状态机
-
马尔可夫过程
状态间转移都引导出一组联立线性方程,它们的解就是在出现 n 次转移之后状态概率的生成函 数.这种系统称为马尔可夫过程
-
考虑不出现模式的的和式
\(1 + N(H + T) = N + S\)
其中的 1 考虑了一次不抛的情况。即 N = 1 + H + T + ... 。如果不考虑这种情况,则
\(H + T + N(H + T) = N + S\)
-
公式 (8.73)
\(NA = S(1 + A^{(1)}[A^{(1)}=A_{(1)}] + A^{(2)}[A^{(2)}=A_{(2)}] + ...)\)
- 公式 (8.74) (8.75) 直接计算期望与方差
- 自我不重叠的模式要比自我有重叠的模式出现得更早
-
Penney 赌注游戏
- 带入 H= T + 1/2,可直接得\(S_A = 2/3, S_B = 1/3\)
-
漂亮的公式

- 散列(没讲)
9 渐进式¶
-
渐进
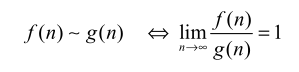
-
量的等级
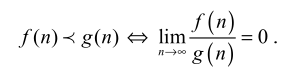
大 O 记号
-
\(f(n) = O(g(n)) \(,则存在常数\)C\)
\(|f(n)| \le C|g(n)|, n\ge n_0\)
- 单向等号:等于号实际上表示集合包含于
O 运算规则
- \(O(O(f)) = O(f)\)
- \(O(f)O(g) = O(fg) = fO(g)\)
-
幂级数截断原理(只需要 S(z) 对某个非 0 z 绝对收敛)
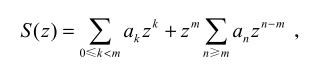
狄利克雷级数截断
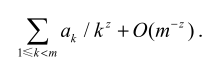
应用
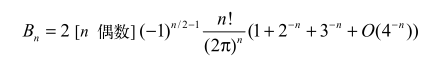
- 截断发散级数所得到的近似公式是有用的
-
表 9-1

-
对于
\(\sqrt{x+1} = 1 + 1/2x -1/8x^2 + 1/16x^3 + O(x^4)\)
-
-
绝对误差,相对误差
\(f + O(g)\), \(f(1+O(g))\)
- 绝对误差与小数点右边正确的十进制数字的个数有关,而相对误差则对应于正确的“有效数字”的个数
- 斯特林公式的绝对误差为\(O(n^{n-3.5}e^n)\)
- 相对误差形式为
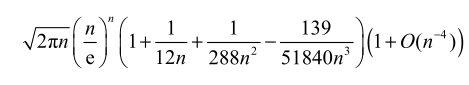
- 抽出最大的部分
-
问题 2:斯特林公式的扰动法
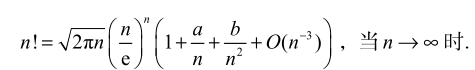
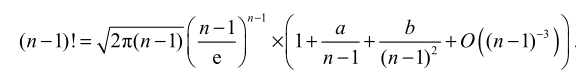
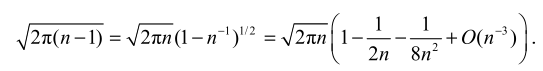
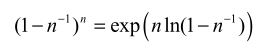
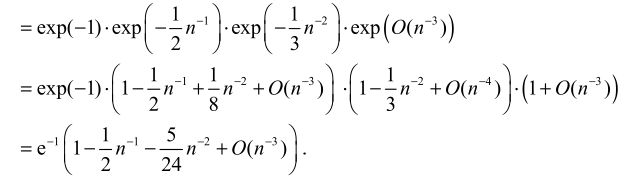
-
问题 3:第 n 个素数
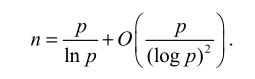
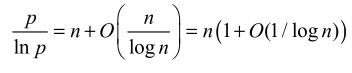
(9.44)
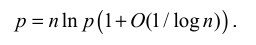
(9.45)
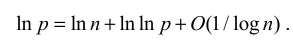
接下来去除 (9.45) 右侧的 p,利用\(p = O(n^2)\)
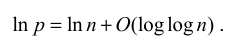
再由 (9.45)
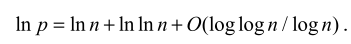
带入 (9.44)
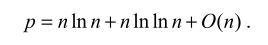
-
问题 4:以前期末考试中的和式
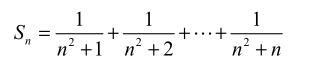
方式一:
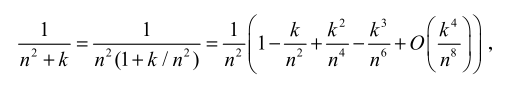
方式二:
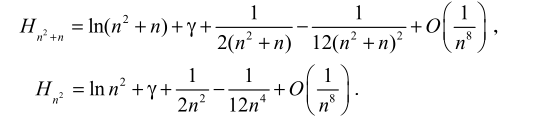
-
问题 5:无限和式

精妙的转换
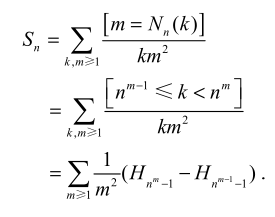
分组
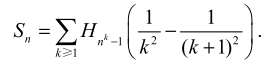
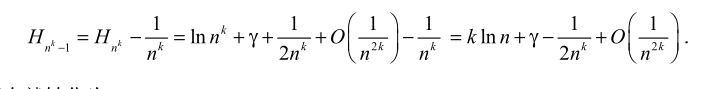
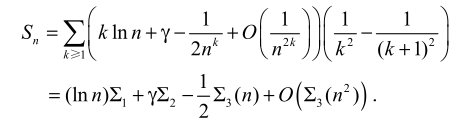
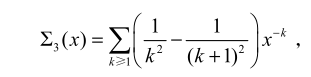
可以截断
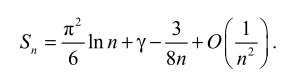
-
问题 6:大 \(\Phi\)
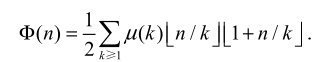
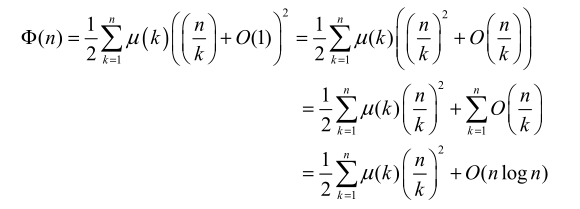
计算
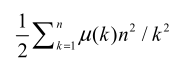 时,
时,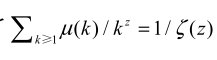
新加的项
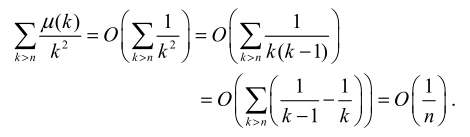
两个渐进技巧¶
-
自助法
-
生成函数求导,得到递推式
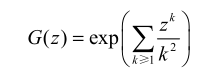
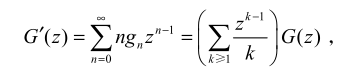
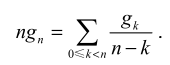
- 一个不等式
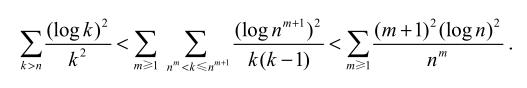
-
欧拉求和公式¶
-
形式上的证明
\(\Delta = e^D - 1\)
\(\Sigma = \frac{1}{\Delta} = \frac{1}{e^D - 1} = \frac{1}{D} \hat{B}(D)\)
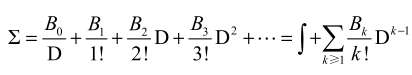
-
归纳法证明
-
只需证明 a=0, b= 1 时成立
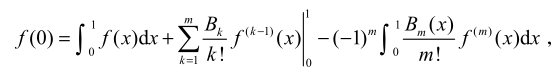
-
则 L 时,有

-
-
伯努利多项式
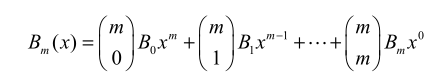
-
对 m 进行归纳
-
m = 0
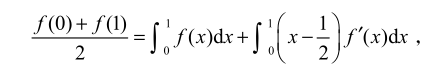
-
-
-
伯努利多项式总结
-
可以分析出单调性,正负性以 4 为周期。
- 0,1 上积分为 0
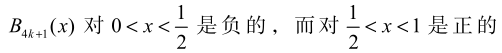
- \(B_{4k+1}\)的积分对应\(B_{4k+2}/4k+2\),可以分析出\(B_{4k+2}\)的单调性
- 有
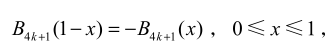
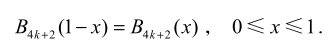
- 从而\(B_{2m}\)在 0,1 上最大值在 0 或 1/2 处取得
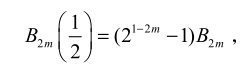
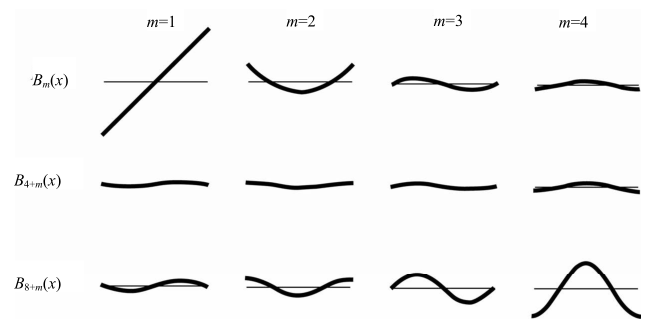
-
-
欧拉求和公式
- 9.78
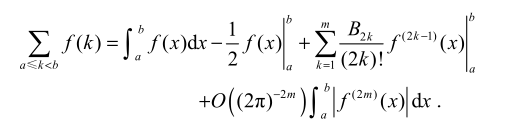
-
再次改进
- 余项将位于 0 第一个被抛弃的项之间
- 好像有前提条件
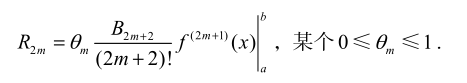
-
简单的常数项版欧拉求和公式
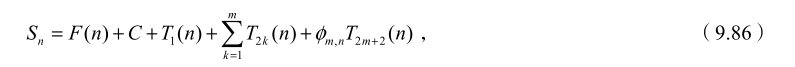
-
调和级数
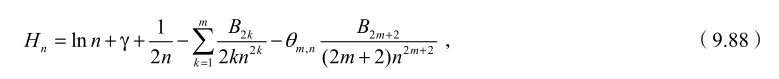
-
斯特林公式
- 斯特林常数
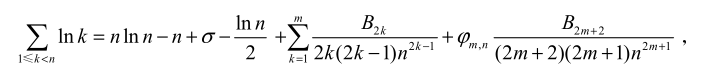

- 9.78